Score function -> Loss function -> Optimization.
Recall that SVM was formulated as:
This formula archieves a very low loss L. Optimization is the process of finding the set of parameters W that minimize the loss function.
Visualizing the loss function
For high-dimensional spaces, linear classifier weight matrix is difficult to visualize. However, we can gain some intuitions about one by slicing through the high-dimensinal space along rays(1-dimension) or along planes(2-dimensions).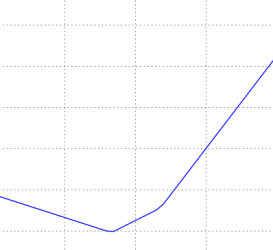
Left: one-dimensional loss by only varying a. Middle and Right: two-dimensional loss slice, Blue = low loss, Red = high loss. The loss is piecewise-linear structure.
For single example, we have:

We can visualize this as follows: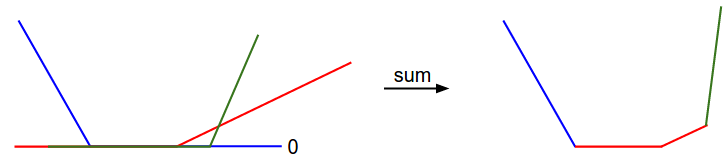
x-axis is a single weight and y-asix is the loss.
Th picture above has shown an example of a convex function.
Optimization
The goal of optimization is to find W that minimizes the loss function.
Strategy 1: Random search(very bad)
Try out many different random weights and keep track of what works best.
Strategy 2: Random local search
Start out with a random W, generate random perturbations &W to it and if the loss is lower.
This strategy is better, but still wasteful and computationally expensive.
Strategy 3: Following the Gradient
Find a direction in the weight-space that would improve our weight vector. I means we can compute teh best direction along which we should change our weight vector that is mathematically guaranteed to be the direction of the steepest descend.
In one-dimensional functions, the mathematically expression is:
Gradient check: unlike the numerical gradient it can be more error prone to implement, which is why in practice it is very common to compute the analytic gradient and compare it to the numerical gradient to check the correctness of your implementation.
SVM loss function for a single datapoint:
We can differentiate the function with respect to the weights.
Gradient descent
Mini-batch gradient descent: batch training
Stochastic gradient descent(or on-line gradient descent): mini-batch contains only a single example.